गणित की अवधारनाएं अमूर्त होती हैं, एक विचार रूप में ,जो मानव की एक समझ हैं । कुछ सर्व सिद्ध मान्यताएँ जो स्वयं सिद्ध है, या जिन्हे सिद्ध नहीं किया जा सकता है, उन पर तर्क की सुसंगतता से गणित की अवधारनाए सोपानक्रमिकता से आगे बढ़ती जाती हैं ।

जाँच और आगमनात्मक तर्क गणितीय सिद्धांतों को खोजने के महत्वपूर्ण तरीके होते हैं लेकिन ये दोषमुक्त नहीं होते, और इसलिए हमें निगमनात्क तर्कों और ‘प्रमाणों’ की आवश्यकता होती है।

इस विचार तक समझ निर्मित करने के लिए विद्यार्थी ऐसी गतिविधियों से शुरुआत करते हैं जिनमें   भिन्न पैटर्नों का अवलोकन करके कुछ अनुमान लगाना होते हैं। वे विभिन्न उदाहरणों में अपने अनुमानों को जाँचते हैं, और इस प्रकार जाँच तथा प्रमाण के बीच के भेद को समझना शुरू करते हैं। एक सक्रिय गतिविधि के द्वारा वे इस बात को भी जान लेते हैं कि किसी अनुमान को असत्य प्रमाणित करने के लिए एक ही विपरीत उदाहरण पर्याप्त होता है। उन् यह भी पता हें चलता है कि किसी अनुमान को निर्णायक रूप से ‘प्रमाणित’ करने के लिए आगमनात्मक तर्क पर्याप्त नहीं होते।

  एक  उदाहरण से बात और स्पष्ट होगी , अभी हाल में ही  मेरे मित्र ने एक नई बात मेरी जानकारी में जोड़ी –

Perfect नंबर से जुड़ी हुई, उसका कहना था की किसी भी perfect नंबर का बीजांक 1 होगा

, यह मेरे लिए बड़ी मजेदार बात थी । पर्फेक्ट नंबर उस संख्या को कहते हैं जिसके भाजकों का योग वही संख्या होती है, भाजकों में स्वयं को नहीं गिनेंगे, उदाहरण से बात और साफ होगी –

28 –  1+2+4+7+14

B (28) = B (10) = 1

B (496) = B (19) =1

B (8128) = B (19) = 1

B (33550336) = B (29) =1

इस पर मेरे मन तुरंत यह सवाल आया की 6 भी तो पर्फेक्ट नंबर है (6=1+2+3),पर इसका बीजांक तो 6 ही हैं। तो हम पर्फेक्ट नंबर का बीजांक 1 होगा कैसे कह सकते हैं ?

गणित में कई बार ऐसा होता है की कुछ उदाहरण हमें किसी समान्यकरण की ओर ले जाते हैं,पर अचानक से कोई प्रतिउदाहरण आते ही हमारी बनाई इमारत तुरंत ढह जाती है । एक मुक्कमल गणितिए तर्क के बिना हम गणित में कोई समान्यकरण नहीं कर सकते।

कक्षा में बच्चों के साथ प्रमाण की आवयशकता पर बातचीत के लिए हम इस तरह प्रयास कर सकते हैं –

विद्यार्थी एक वृत्त बनाएं और उस पर दो सुस्पष्ट बिन्दु बनाएं और फिर इन बिन्दुओं को मिलाने से बने क्षेत्रों की संख्या पर ध्यान दें। फिर यही प्रक्रिया वे 3, 4, 5 बिन्दुओं के साथ दोहराएं। विद्यार्थी हर बार बने पृथक क्षेत्रों की संख्या गिनें और देखें कि क्या वृत्त पर बिन्दुओं  की संख्या और उनसे बन रहे पृथक क्षेत्रों की संख्या के बीच कोई खास व्यवस्था/ संबंध दिखाई देते हैं। उन्हें क्या लगता है कि यह नियम वृत्त पर बिन्दुओं की कितनी भी संख्या के लिए सही होगा। उनसे उनके जवाब के कारण पूछें। विद्यार्थियों से कहें कि वे वृत्त पर बिन्दुओं की अलग-अलग संख्या के साथ इसकी जाँच करें, और अपने अवलोकनों के आधार पर, अगर जरूरत पड़े, तो अपने पहले दिए गए उत्तर को बदल दें।

• Save

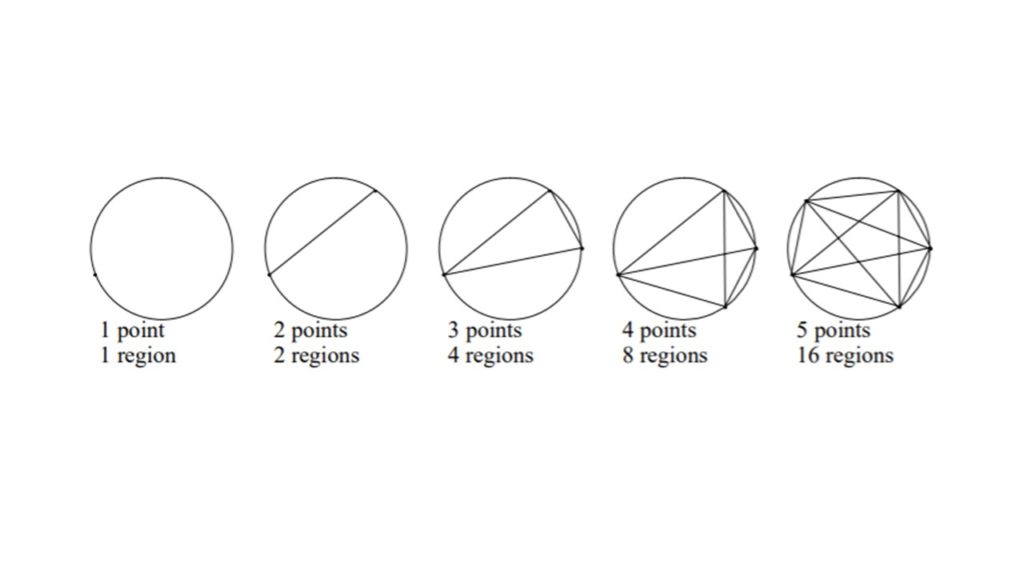
आप विद्यार्थियों से निम्नलिखित सवाल पूछ सकते हैं :

• सामान्य नियम से वे क्या समझे?

 • क्या किसी अनुमान को सिर्फ उदाहरण देकर सत्य सिद्ध किया जा सकता है? हमें कितने उदाहरण देना चाहिए? / किसी अनुमान को सत्य सिद्ध करने के लिए कितने उदाहरण काफी होते हैं?

• हम कैसे मान सकते हैं कि हमारे उदाहरणों के कोई विपरीत उदाहरण नहीं होंगे?

• हम किसी अनुमान को असत्य कैसे सिद्ध कर सकते हैं? इसके लिए हमें कितने विपरीत उदाहरणों की जरूरत होगी?

 • आप उनसे यह भी पूछ सकते हैं कि उन्हें प्रमाण क्यों महत्वपूर्ण लगते हैं।

  इस बात को समझने में विद्यार्थियों की मदद करें कि किसी अनुमान को सिर्फ उदाहरणों के आधार पर ही निर्णायक रूप से सत्य नहीं कहा जा सकता। पहले कुछ उदाहरणों में, क्षेत्रों की संख्या 2 ^{n -1} है जहाँ n वृत्त पर बने बिन्दुओं की संख्या है। (इस बात से कोई दिक्कत नहीं है अगर विद्यार्थी चिन्हों वाले इस औपचारिक संकेतन के बजाय किसी व्यवस्था को व्यक्त करने के लिए भाषा का उपयोग करें और उसे ‘नियम’ की तरह व्यक्त करें)। लेकिन यह व्यवस्था n=6 पर आकर गलत सिद्ध हो जाती है जो यह दिखाता है कि उदाहरणों द्वारा लगाया गया अनुमान हमेशा सच हो ऐसा जरुरी नहीं है। इससे विद्यार्थियों को इस तथ्य को समझने में मदद मिलती है कि किसी अनुमान को कितने भी उदाहरणों द्वारा सही सिद्ध नहीं किया जा सकता – अपने अनुमान को सही सिद्ध करने के लिए उन्हें निगमनात्मक तर्क देना जरूरी है।

• Save

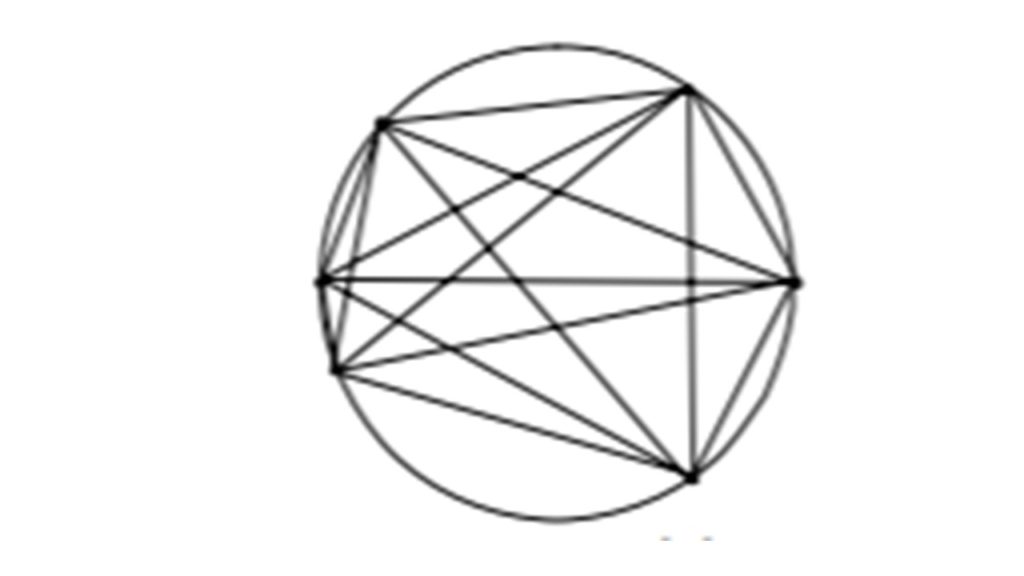
अभी हम गणित के एक पहलू पर बात कर रहे थे जहां सब कुछ निश्चितता की ओर है, प्रमाण इसे और भी सुंदर बना देता है। पर अब गणित को एक ओर नजरिए से देखते हैं जहां निश्चित जैसा कुछ नहीं है, प्रमाण की आवयशकता कहीं कोने में दुबक जाती है और रह जाती है बड़े समूह की सहूलियत के लिए कोरी मान्यताएँ। गणित की प्रकृति और इसे पढ़ाने के तरीके गणित को एक निश्चितता की ओर दखेल देते हैं, जहां विवादों और बहस के लिए कोई जगह नहीं है। यहाँ वोट डालकर सच या झूठ का फैसला नहीं किया जाता बल्कि तर्क आधारित होता है, पर इस लेख में गणित की दुनिया के कुछ ऐसे उदाहरण साझा कर रहा हूँ जो गणित को इतना निश्चित मानने की सोच को हिलाने का माद्दा रखते हैं। आप पाएंगे की गणित भी एक बड़े समूह की मान्यताओं से चल रहा है जैसे भाषा या अन्य विषयों में की ज्यादा लोग किसे सही मानते हैं को मानक बना लिया जाता है। आइये कुछ उदाहरणों को देखते हैं –

दैनिक जीवन की समस्याओं को गणितीय प्रतीकों के रूप में लिखना और इसके उलट गणितीय प्रतीकों को दैनिक जीवन से जोड़कर सामान्य भाषा में व्यक्त करना गणित सीखने का महत्वपूर्ण लक्ष्य  है।

3×4 जो की गणितीय प्रतीकों में लिखा है, इसके हम कितने तरीकों से समझ सकते हैं-

3 multiplied by 4                       3 गुना 4

3 time 4                             3 बार 4

3 fours                               3 चार

3 by 4                                3 बाई 4

4 by 3                                4 बाई 3

4 threes                              4 तीन

3 lots of 4                           4 के 3 समूह

4 lots of  3                          3 के 4 समूह

3 timesed by 4                       4 बार 3

इन सभी निरूपण को दो वर्गो में बाँट सकते हैं –

•  

4 अवयवो का एक समूह जिसे 3 बार दोहराया गया है

• Save

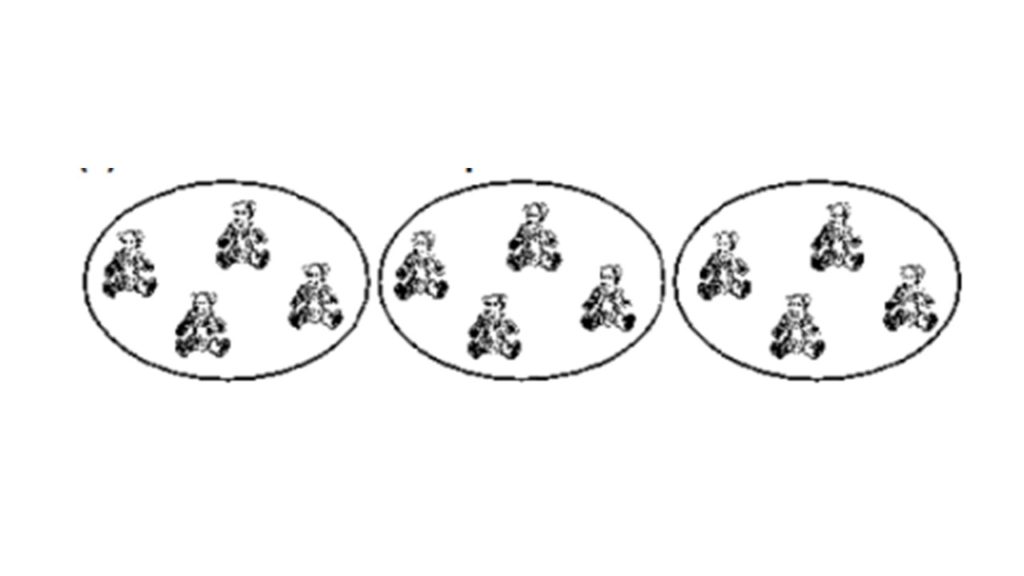
3 time 4    

3 fours    

4 by 3     

3 lots of 4                                                                                                         

•  

3 अवयवो का एक समूह जिसे 4 बार दोहराया गया है 

• Save

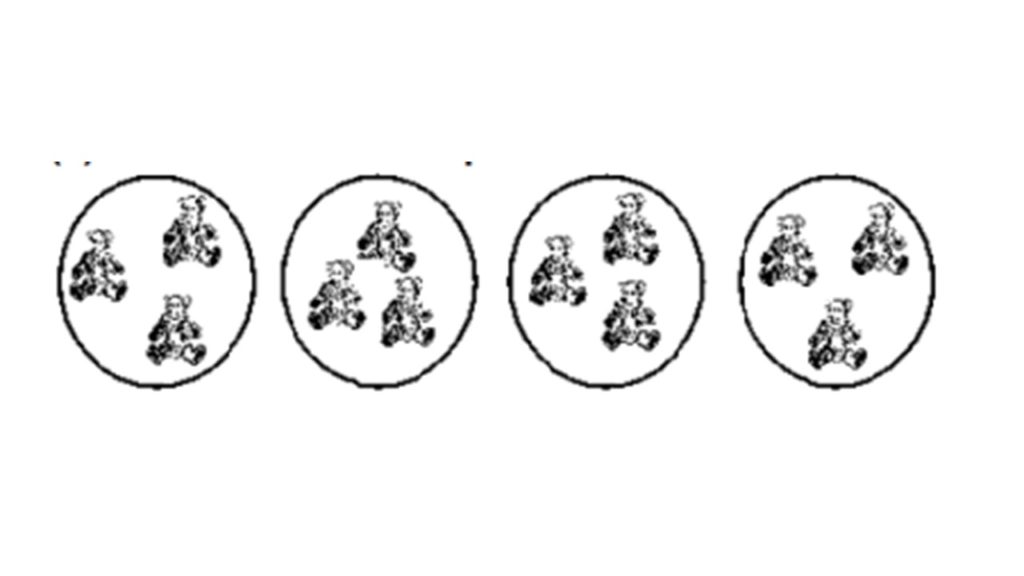
3 multiplied by 4   

3 by 4

4 threes

3 timesed by 4                            

क्या इन दोनों ही तरीकों को उचित माना जाये? या कोई एक तरीका ही उचित है?

हम देखते हैं की जैसी निश्चितता को हम गणित से जोड़कर देखते हैं, यहाँ उस पर प्रश्न चिन्ह लगता है? हम अक्सर ये कहते सुनते हैं या स्वयं भी कह देते हैं की गणित में 2 और 2 चार ही होता है, कुछ और नहीं हो सकता है, इस जुमले का आशय यही होता है की गणित बिल्कुल स्पष्ट है, यहाँ संशय नहीं होता है।

गणित की यही विशेषता इसे अन्य विषयों से विशिष्ट बनाती है और जटिल भी। पर यहाँ मैं प्राथमिक गणित से कुछ ऐसे उदाहरण पर बात कर रहा हूँ जो गणित की इस निश्चितता को चुनौती देती है, आप किस तर्क से सहमति रखते हैं और आपकी सहमति व असहमति के क्या आधार है, साझा जरूर करें?

इस प्रक्रिया में हम महत्वपूर्ण गणित कर रहे होंगे और केवल सही जबाब नहीं, प्रक्रिया महत्वपूर्ण है इससे ही गणित विषय में जीवंतता बनी रहती है।

3×4 के लिए कौन सा संदर्भ उचित है- a व b?

आइये एक तर्क को देखते हैं-

गणित में हर प्रतीक का अपना विशिष्ट अर्थ होता है, × के प्रतीक की  भी एक ही उचित व्याख्या है –

× मतलब है multiplied by (गुना होना)

×4 एक गुणन संक्रिया है जो 3 के समूह पर आरोपित की गयी है, इस प्रकार   3 अवयवो का एक समूह जिसे 4 बार दोहराया गया है, 3×4 की उचित व्याख्या है।

पर जब हम इस पर और जानना चाहते हैं तो गूगल पर भी खोजते हैं, विकिपीडिया को भी टटोलते हैं पर गूगल या विकिपीडिया को लोग औपचारिक माध्यम नहीं मानते हैं पर सबसे ज्यादा सूचनाएँ इन्ही माध्यमों से लेकर उपयोग करते हैं।

गुण्य × गुणक = गुणनफल

गुण्य व गुणक को गुणज भी कहते हैं,

4 multiplied by 3  को 3×4  से निरूपित किया गया है और इसे 3 बार 4 भी कहा गया है, और बताया गया है की गुण्य या गुणक में कौन पहले आएगा ये निश्चित नहीं है दोनों तरीके से ही उपयोग में लाया जाता है। यहाँ हम देखते हैं की जिस उदाहरण से हमने अपनी बात शुरू की थी और एक नतीजे पर पहुंचे थे की  ×4 एक गुणन संक्रिया है जो 3 के समूह पर आरोपित की गयी है, इस प्रकार   3 अवयवो का एक समूह जिसे 4 बार दोहराया गया है, 3×4 की उचित व्याख्या है- से विसंगति है।

• Save

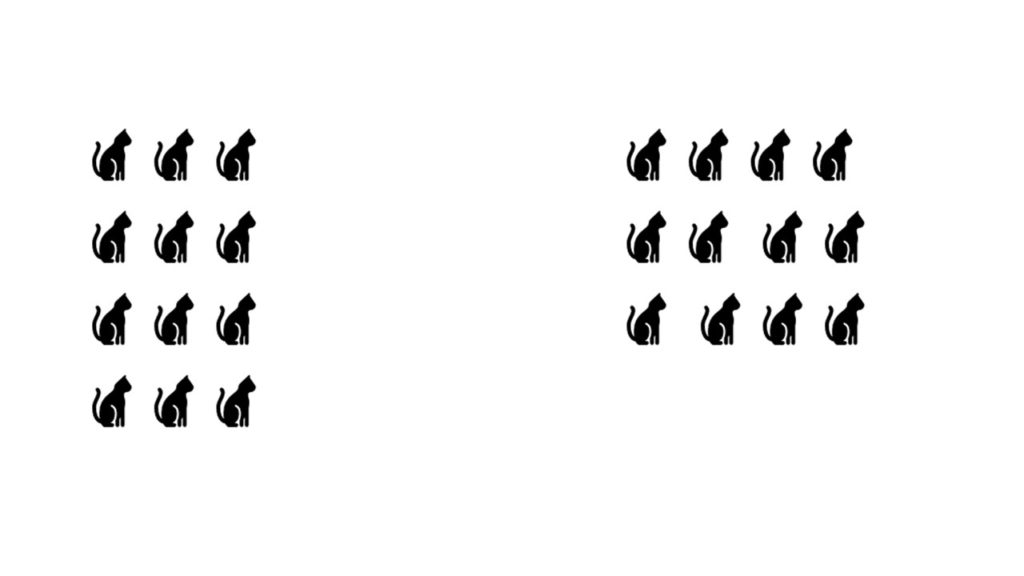
पर गणित तो एक विशिष्ट भाषा है, एक निरूपण के दोनों अर्थ ठीक होना थोड़ा असहज करता है, यदि किसी मशीन को निर्देश दिये जाएंगे तो वो कौन से अर्थ का अनुपालन करेगी? क्या दोनों अर्थो में से कोई भी मान लेने से समान परिणाम मिलेगा?

3×4 का अर्थ 3 पंक्ति और 4 स्तम्भ और 4×3 का अर्थ 4 पंक्ति और 3 स्तम्भ है? क्या हम दोनों को एक ही मान सकते हैं या दोनों एक ही होते हैं?  आपका क्या नजरिया है?

आइये चर्चा को आगे बढ़ाते हैं-

प्राथमिक कक्षाओं को जब पहाड़े सिखाते हैं तो आप किस तरह से लिखते हैं –

1×3=3

2×3=6

3×3=9

4×3=12

5×3=15

6×3=18

7×3=21

8×3=24

9×3=27

10×3=30

या

3×1=3

3×2=6

3×3=9

3×4=12

3×5=15

3×6=18

3×7=21

3×8=24

3×9=27

3×10=30

क्या दोनों तरीके उचित हैं? क्या इससे अवधारणा पर कोई फर्क नहीं पड़ता है?

या गणित में लिखे गए क्रम का एक विशिष्ट अर्थ होता है? यदि हम इसको भाषा व चित्र में निरूपित करें तो क्या वो एक सा होगा?

4×3

3 अवयवों के 4 समूह

• Save

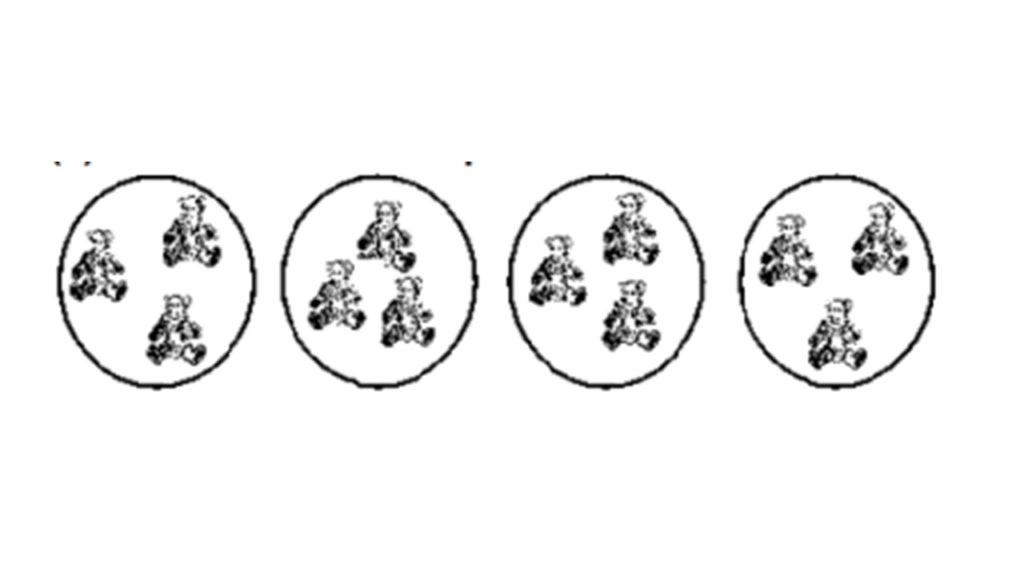
अगर हम इस निरूपण का अनुसरण करते हैं तो × के निशान से पहले लिखी संख्या समूह को व्यक्त करती है और × के निशान के बाद की संख्या समूह में अवयवों को व्यक्त करती है। ऊपर दिये गए उदाहरण में 4 समूह हैं, जिसमें प्रत्येक में 3-3 अवयव हैं।

जब हम पाठ्य पुस्तकों का अवलोकन करते हैं (एनसीईआरटी, उत्तर प्रदेश इत्यादि ) तो पाते हैं की वो भी इसी निरूपण का अनुसरण करती हैं। पर हम पुरानी पुस्तकों व कई अन्य जगह जैसे समान्यत: अपने स्कूल में पहाड़े बोलते समय दूसरे तरीके को भी पाते हैं, इससे ये प्रश्न सामने आता है की इनमें से सही क्या है? यदि मैं बच्चों को पहाड़े सिखाना चाहता हूँ तो किस तरीके का अनुसरण करूँ?

यदि दोनों तरीके उचित हैं तो क्या पाठ्य पुस्तक में दिये गए तरीके को व्यावहारिक चलन मानकर इस पर कार्य करना उचित होगा?

आमतौर पर बच्चे गुणा व पहाड़ो की अवधारणा से परिचय कक्षा 2 ( 6 या 7 वर्ष की आयु में) में असंबंधित तथ्यों की श्रंखला के रूप में करते हैं, बच्चों को ये तथ्य याद कर लेने होते हैं, इसलिए 5वीं कक्षा के बच्चे भी 28×3 को हल जानने बाद 29×3 नहीं बता पाते।  

इसी प्रकार गुणा के मानक एल्गॉरिथ्म में दूसरी पंक्ति में × लगाएँ या 0 या खाली छोड़ देना चाहिए, इस पर भी कोई एक मत नहीं हो पाता है।

आइये ज्यामिती से भी एक उदाहरण लेते हैं,

वृत एक दो विमीय आकृति है – क्या इस पर भी संशय किया जा सकता है? 

वृत की परिभाषा के अनुसार -यह एक निश्चित बिन्दू से निश्चित दूरी का बिन्दू पथ वृत होता है, इसमें इसके अंदर के क्षेत्रफल को शामिल करने की बात नहीं है।ये जो परिधि है यही वृत्त है- जो एक विमीय है, इसके अंदर या बाहर का भाग वृत्त नहीं है।

एक अन्य तर्क ( सम्मिश्र संख्याए) की सहायता से वृत्त को एक विमीय बताया जा सकता है.

दो विमीय होने के भी तर्क दिये गए- x व y अक्ष की सहायता से, आकृतियाँ  जिनका क्षेत्रफल होता है  द्विविमीय होती हैं जैसे त्रिभुज, चतुर्भुज, वृत्त  आदि  व आकृतियाँ जिनका आयतन होता है- घन, घनाभ, बेलन आदि   त्रि विमीय होती हैं ।

गणित का ज्ञान सार्वभौमिक होता है और तर्क पर आधारित होता है उसे हमारी सहमति या असहमति प्रभावित नहीं करती है, पर हम पाते हैं की गणित में भी यदाकदा convention बनाए गए हैं, और निरंतर गणितीय ज्ञान में अविरल विकास होता रहा है और परिष्कृत भी होता रहा है, गणित में  भी सब कुछ शाश्वत सत्य या निश्चितता ज्ञान की सभी शाखाओं की तरह  नहीं है।